Finding the Higgs Boson - Discovering the Higgs Boson

These data are taken from Wunsch (2021), which uses simulations to reproduce the 2012 CMS data.

%matplotlib widget
import awkward as ak
import numpy as np
import hist
import particle
import hepunits
import ipywidgets
from matplotlib import pyplot as plt
plt.ioff()

import vector
vector.register_awkward()

Load some data

raw_events = ak.from_parquet("data/SMHiggsToZZTo4L.parquet")

raw_events.type.show()

299973 * {
    run: int32,
    luminosityBlock: int64,
    event: uint64,
    PV_npvs: int32,
    PV_x: float32,
    PV_y: float32,
    PV_z: float32,
    nMuon: int64,
    Muon_pt: var * float32,
    Muon_eta: var * float32,
    Muon_phi: var * float32,
    Muon_mass: var * float32,
    Muon_charge: var * int32,
    Muon_pfRelIso03_all: var * float32,
    Muon_pfRelIso04_all: var * float32,
    Muon_dxy: var * float32,
    Muon_dxyErr: var * float32,
    Muon_dz: var * float32,
    Muon_dzErr: var * float32,
    nElectron: int64,
    Electron_pt: var * float32,
    Electron_eta: var * float32,
    Electron_phi: var * float32,
    Electron_mass: var * float32,
    Electron_charge: var * int32,
    Electron_pfRelIso03_all: var * float32,
    Electron_dxy: var * float32,
    Electron_dxyErr: var * float32,
    Electron_dz: var * float32,
    Electron_dzErr: var * float32,
    MET_pt: float32,
    MET_phi: float32
}

Let’s restructure this to take advantage of structural operations.

def make_record_from_prefix(arr, prefix, name):
    prefix_with_separator = f"{prefix}_"
    arr_items = ak.unzip(arr, how=dict).items()
    structure = {
       n.removeprefix(prefix_with_separator): v for n, v in arr_items
       if n.startswith(prefix_with_separator)
    }
    return ak.zip(structure, with_name=name)

events = ak.zip({
    "muons": make_record_from_prefix(raw_events, "Muon", "Momentum4D"),
    "electrons": make_record_from_prefix(raw_events, "Electron", "Momentum4D"),
}, depth_limit=1)

events.type.show()

299973 * {
    muons: var * Momentum4D[
        pt: float32,
        eta: float32,
        phi: float32,
        mass: float32,
        charge: int32,
        pfRelIso03_all: float32,
        pfRelIso04_all: float32,
        dxy: float32,
        dxyErr: float32,
        dz: float32,
        dzErr: float32
    ],
    electrons: var * Momentum4D[
        pt: float32,
        eta: float32,
        phi: float32,
        mass: float32,
        charge: int32,
        pfRelIso03_all: float32,
        dxy: float32,
        dxyErr: float32,
        dz: float32,
        dzErr: float32
    ]
}

H → ZZ* → 4μ or 4e¶

Find events consisting of four same-flavour leptons

four_muons = ak.combinations(events.muons, 4)
four_electrons = ak.combinations(events.electrons, 4)

Compute the invariant mass of the frame

M_0^2 = \left(\sum_i E_i\right)^{2}-\left\|\sum_i \mathbf {p}_i\right\|^{2}

(1)

by adding together all of the four-momentum vectors

p=\left(p^{0},p^{1},p^{2},p^{3}\right)=\left({\frac {E}{c}},p_{x},p_{y},p_{z}\right).

(2)

four_muons_mass = (four_muons['0'] + four_muons['1'] + four_muons['2'] + four_muons['3']).mass
four_electrons_mass = (four_electrons['0'] + four_electrons['1'] + four_electrons['2'] + four_electrons['3']).mass

Histogram the result

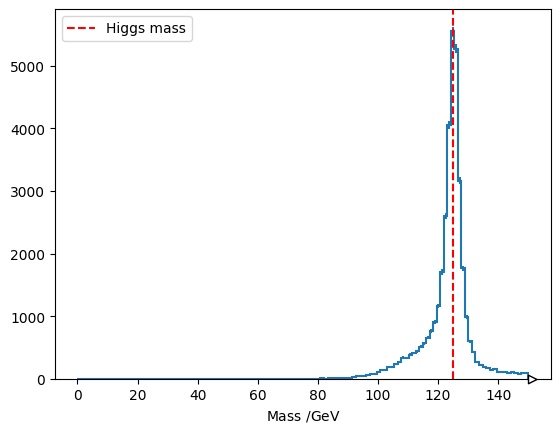
fig, ax = plt.subplots()
(
    hist.Hist.new.Reg(128, 0, 150, label="Mass /$\\text{GeV}$")
    .Double()
    .fill_flattened(four_muons_mass)
    .fill_flattened(four_electrons_mass)
).plot(ax=ax)
ax.axvline(125.11, linestyle='dashed', color="red", label="Higgs mass")
plt.legend()
plt.show()

H → ZZ* → 2μ2e¶

muons_plus = events.muons[events.muons.charge > 0]
muons_minus = events.muons[events.muons.charge < 0]

electrons_plus = events.electrons[events.electrons.charge > 0]
electrons_minus = events.electrons[events.electrons.charge < 0]

muon_plus, muon_minus, electron_plus, electron_minus = ak.unzip(
    ak.cartesian(
        (muons_plus, muons_minus, electrons_plus, electrons_minus)
    )
)

fig, ax = plt.subplots()
(
    hist.Hist.new.Reg(128, 0, 150, label="Mass /$\\text{GeV}$")
    .Double()
    .fill_flattened((muon_plus + muon_minus + electron_plus + electron_minus).mass)

).plot(ax=ax)
ax.axvline(125.11, linestyle='dashed', color="red", label="Higgs mass")
plt.legend()
plt.show()

For e+e-e+e- events (or muon equivalent), we can combine e+e- in two pairings. We usually find an “on-shell” Z that has close to the Z mass. We can cut according to this heuristic

ZMASS = particle.Particle.findall("Z0")[0].mass / hepunits.GeV
ZMASS

91.188

def compute_dist(cut):
    is_on_shell_z_muon = np.abs((muon_plus + muon_minus).mass - ZMASS) < cut
    is_on_shell_z_electron = np.abs((electron_plus + electron_minus).mass - ZMASS) < cut
    is_on_shell_z = is_on_shell_z_muon | is_on_shell_z_electron
    distribution = (
        hist.Hist.new.Reg(128, 0, 150, label="Mass /$\\text{GeV}$")
        .Double()
        .fill_flattened(
            (muon_plus + muon_minus + electron_plus + electron_minus).mass[is_on_shell_z]
        )
    )
    return distribution

initial_cut = 20

slider = ipywidgets.FloatSlider(value=initial_cut, min=1, max=100, description="Mass /GeV")

@slider.observe
def fn(change):
    if change['name'] != "value":
        return

    cut = change['new']
    distribution = compute_dist(cut)
    artist.stairs.set_data(
        values=distribution.values()
    )
    fig.canvas.draw()
    fig.canvas.flush_events()

initial_dist = compute_dist(initial_cut)

fig, ax = plt.subplots()
artist, = initial_dist.plot(ax=ax)
ax.axvline(125.11, linestyle='dashed', color="red", label="Higgs mass")
plt.legend()

# Create a placeholder image
from base64 import b64decode

data, metadata = get_ipython().display_formatter.format(fig)
with open("on-shell-zz-2u2e.png", "wb") as f:
    f.write(
        b64decode(data["image/png"])
    )

ipywidgets.VBox([
    fig.canvas,
    slider
])

References¶

Wunsch, S. (2021). SMHiggsToZZTo4L dataset in reduced NanoAOD format for education and outreach. CERN Open Data Portal. 10.7483/OPENDATA.CMS.8FLU.UIQJ